Welcome to Elementary Components

These are the simple components that cannot be decomposed furthermore because they do not contain the internal documents. Their model is described by the constitutive relations between the port efforts and flows, which are stored in the component ports. The Bond Graph theory defines nine such components, which are listed in the table below. The components allow also the control signal ports for either input or output of the signals.

Of these components the first one corresponds to Newton's 2nd law in Mechanics and Faraday's law in Electricity. It contains a dynamic constitutive relation between the element's momentum p and the port's effort. Similarly, the second one is also in the form of a differential equation relating to charge and port flow. A capacitor and mechanical spring are described by such an element.

The constitutive relations of other elementary components are purely algebraic and describe different effects such as the linear friction, the transformers, the gyration effect (such as in DC motors), implied sources of the efforts and flows. The next two elements are specific because they describe the constraints applied to the model. They correspond to Kirchhoff's laws in Electricity. Similar laws are valid in Mechanics, e.g. the equation of rigid body dynamic equilibrium, kinematical relations for the velocities of the rigid body points, etc.

Element Type	Symbol	Constitutive Releations	Note
Inertial		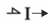dp/dt = e p = I ∙ f	p - internal variable (generalized momentum), I - inertia. The effort is a function of the internal variable.
Capacitive		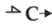dq/dt = f q = e/C	q - internal variable (generalized charge), C - capacitance. The flow is a function of the internal variable.
Resistive		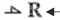e = R ∙ f	R - resitance; a dependence on the input is allowed.
Transfomer		e2 = k ∙ e1 f1 = k ∙ f2	k - a constant or the input function
Gyrator		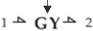e2 = k ∙ f1 e1 = k ∙ f2	k - a constant or the input function
Source Effort		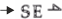e = fun(t, par)	t - time, par - constants, or a dependence on the input.
Source Flow		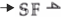f = fun(t, par)	t - time, par - constants, or a dependence on the input.
Effort Branch		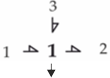e1 ± e2 ± e3 = 0 f1 = f2 = f3	flow junction Take the plus sign if port power is directed into the element, otherwise take the minus sign. The control port picks the common flow variable.
Flow Branch		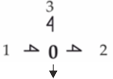e1 = e2 = e3 f1 ± f2 ± f3 = 0	effort junction Take the plus sign if port power is directed into the element, otherwise take the minus sign. The control port picks the common effort variable.