Welcome to Pendulum Problem
As a simple problem to which we will apply Bond Graph modeling, we select well-known
pendulum problem.
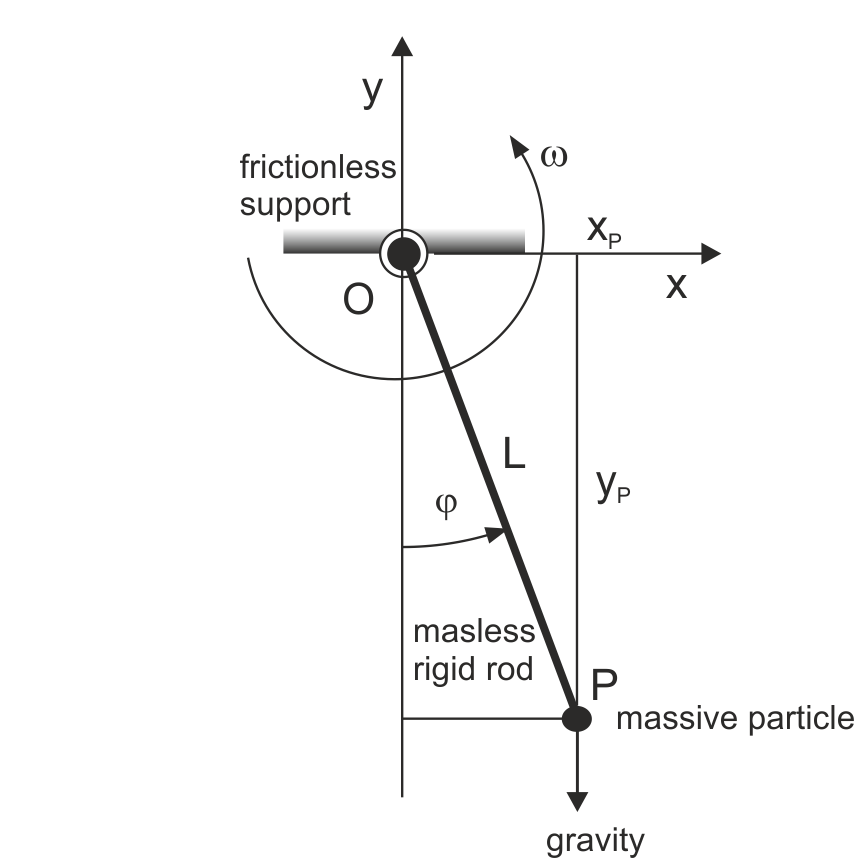
It consists of a massive particle suspended from a support by a massless rod. When displaced from
its vertical position in which its massive particle is in the lowest position and released, it will
swing up and down around its vertical position. Due to friction in the pivot, as well the air resistance,
after some time the energy of the pendulum will dissipate and the pendulum will settle down in the vertical
equilibrium position. The main parameters of the pendulum are (see Figure down below):
• angle φ
with vertical axis,
• angular velocity ω, and
• coordinates of the endpoint x
P and yP.
The pendulum problem is a very old one. The first scientist who studied its properties was a famous Italian scientist Galileo Galilei about 1588. After some sources, he was sparked by the swinging of a chandelier in Pisa Cathedral. Due to fairly small friction in the problem, the friction was usually neglected when treating the pendulum. Galileo experimentally found that the period of oscillation of the pendulum is proportional to the length of the connecting rod. The pendulum was the subject of interest for many other well-known scientists of the past such as Christiaan Huygens, Robert Hook and others.
We will systematically apply the Bond Graph modeling approach to develop a model which follows the functional structure of the pendulum problem. We start from mechanical model of a pendulum.